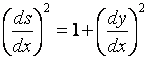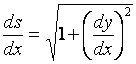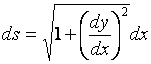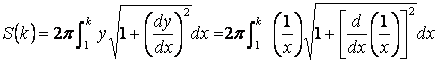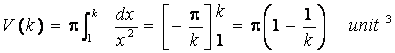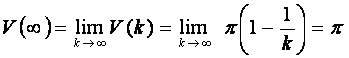Painter’s paradox

It can be shown that the volume of revolution formed by a piece of area can be finite even if the area is infinite! A painter needs infinite amount of paint to paint the surface of a solid with finite volume.

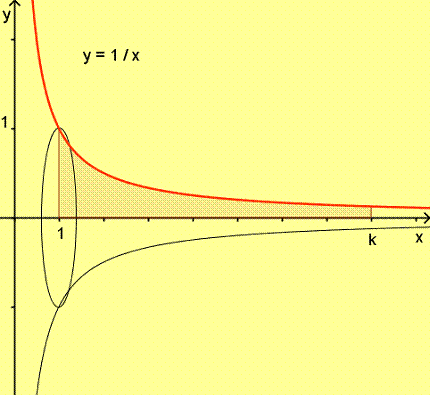
From the above diagram, the curve in red is given by

Let us rotate the curve from x = 1 to x = k .

We like to find the surface area formed by this rotation.

We begin with the “differential Pythagoras Theorem”:

, where ds is the differential arc length

Then

By rotate ds around x-axis by 4 right angles, we get a “belt” with differential surface area:

Hence the surface area can be found by integrating the above:

The volume of revolution about the x-axis is given by :

Put k →∞, we get

(surface area is infinite)

but

(volume is finite)